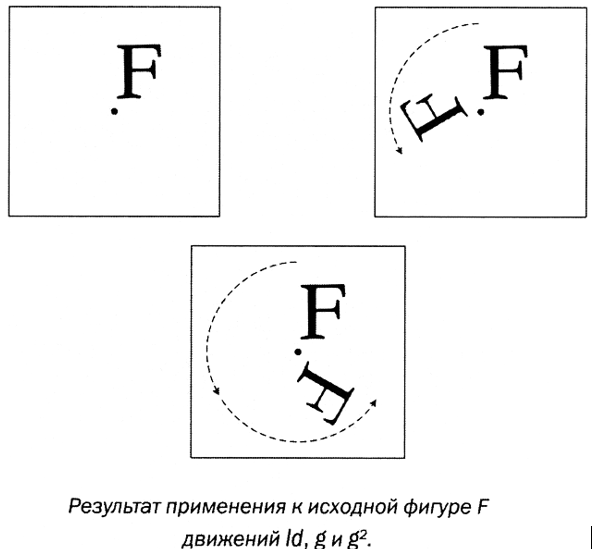
Физика, астрономия, экономика и другие точные науки основаны на математике — это понятно всем. Но взаимосвязь математики и творчества не столь очевидна. А ведь она куда глубже и обширнее, чем думают многие из нас. Математика и творчество развивались параллельно друг другу на протяжении веков. (Например, открытие математической пер­спективы в эпоху Возрождения привело к перевороту в живописи.)

ПОНЯТИЕ ГРУППЫ

Группа в математике – это множество G, на котором определена операция ·. Говорят, что множество G с заданной на нем операцией · (G, ·) является группой, если они обладают следующими свойствами.

1.  Операция является внутренней, то есть результатом этой операции с любыми двумя элементами множества будет элемент этого же множества.

2.  Операция является ассоциативной. Иными словами, для любой тройки элементов группы результат операции над ними одинаков вне зависимости оттого, в каком порядке она будет выполняться.

      3.  Наличие нейтрального элемента. Существует единственный элемент

такой, что

4.  Наличие обратного элемента.

Для любого элемента х группы существует элемент х’ такой, что

Изометрия – это геометрическое преобразование, оставляющее неизменным расстояния между элементами множества.

Иными словами, изометрия – это «жесткое» перемещение, которое не деформирует множество. Примерами изометрии на плоскости являются поворот вокруг точки, параллельный перенос и осевая симметрия (отражение). Изометрией также считается скользящая симметрия – контаминация параллельного переноса и осевой симметрии, ось которой параллельна направлению переноса.

Группы Леонардо – это группы движений с конечным числом элементов и точкой, положение кото­рой остается неизменным вне зависимости от применяемого движения. Группы Леонардо содержат только повороты и различные виды отражений (зеркальной симметрии).

Существует два вида групп Леонардо. Первый – циклические группы, состоящие из одного пово­рота на некоторое число градусов, причем 360° делится на это число без остатка. Примером такой группы является С₃, содержащая поворот g на 120°. Элементами этой группы являются:

где Id – нейтральный элемент.

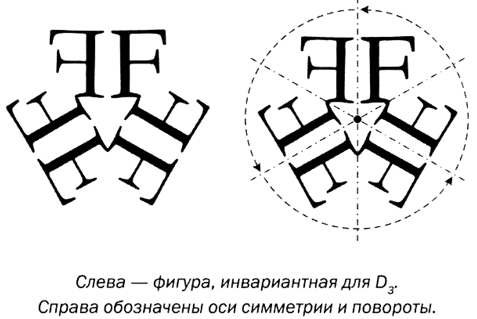
Ко второму типу относятся так называемые диэдрические группы, образованные поворотом и сим­метрией, ось которой проходит через центр вращения. Такие группы обозначаются D_n.

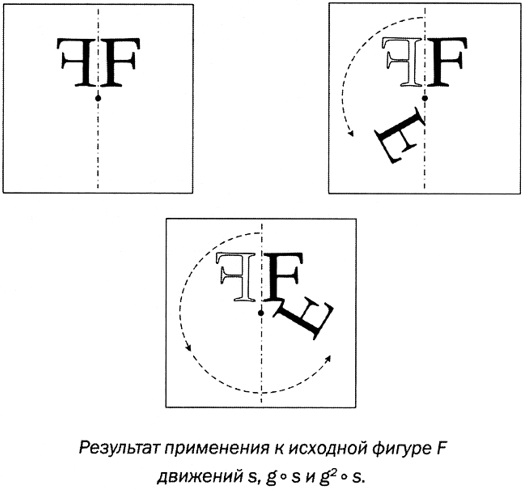
Например, D₃ состоит из поворота g на 120° и симметрии s. Элементами этой группы являются

Группа D₁ образована единственной симметрией.

По материалам книги: